
, where '1/a' is its first term and 'd' is the common difference of the arithmetic sequence a, a + d, a + 2d.
#Arithmetic and geometric sequences and series series#
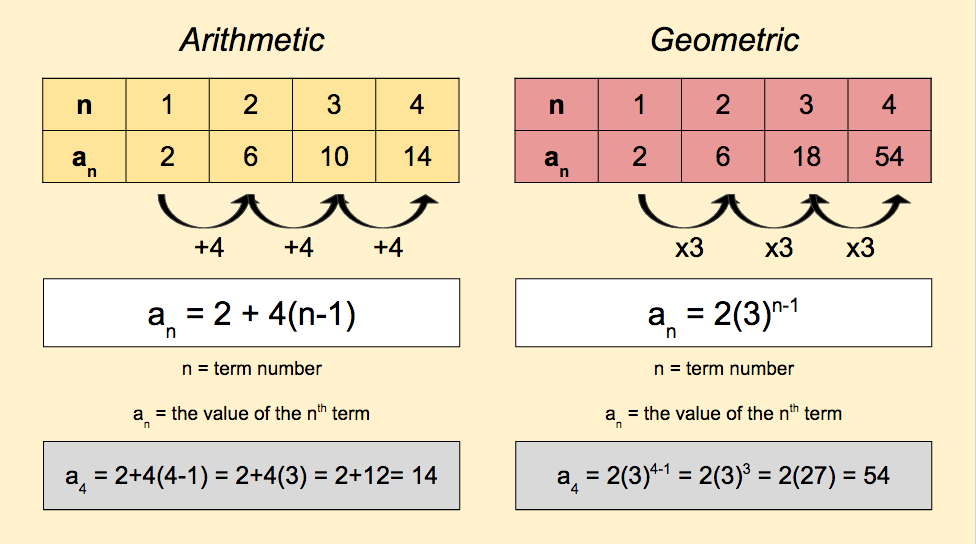
Sum of the finite geometric series (sum of first 'n' terms), S n = a (1 - r n) / (1- r).n th term of geometric sequence, a n = a r n - 1., where 'a' is the first term and 'r' is the common ratio. Sum of the arithmetic series, S n = n/2 (2a + (n - 1) d) (or) S n = n/2 (a + a n)Ĭonsider the geometric sequence a, ar, ar 2, ar 3.n th term of arithmetic sequence, a n = a + (n - 1) d., where 'a' is its first term and 'd' is its common difference. Arithmetic Sequence and Series FormulasĬonsider the arithmetic sequence a, a+d, a+2d, a+3d, a+4d. Let us see each of these formulas in detail and understand what each variable represents. The figure below shows all sequences and series formulas. In a harmonic sequence, the reciprocals of its terms are in an arithmetic sequence. In a geometric sequence, there is a common ratio between consecutive terms. In an arithmetic sequence, there is a common difference between two subsequent terms. to find the sum of the n terms of the series.to find the n th term of the sequence and.Here the sequence and series formulas include formulas The below list includes sequences and series formulas for the arithmetic, geometric, and harmonic sequences. The sequence and series formulas generally include the formulas for the n th term and the sum. A sequence is the set of ordered elements that follow a pattern and a series is the sum of the elements of a sequence. At the end of the first year you will have a total of: \ With simple interest, the key assumption is that you withdraw the interest from the bank as soon as it is paid and deposit it into a separate bank account.Sequence and series formulas are related to different types of sequences and series in math. You are paid $15\%$ interest on your deposit at the end of each year (per annum). We refer to $£A$ as the principal balance.
Simple and Compound Interest Simple Interest For example, \ so the sequence is neither arithmetic nor geometric.

A series does not have to be the sum of all the terms in a sequence. The starting index is written underneath and the final index above, and the sequence to be summed is written on the right. We call the sum of the terms in a sequence a series. The Summation Operator, $\sum$, is used to denote the sum of a sequence. If the dots have nothing after them, the sequence is infinite. If the dots are followed by a final number, the sequence is finite. Note: The 'three dots' notation stands in for missing terms. is a finite sequence whose end value is $19$.Īn infinite sequence is a sequence in which the terms go on forever, for example $2, 5, 8, \dotso$. For example, $1, 3, 5, 7, 9$ is a sequence of odd numbers.Ī finite sequence is a sequence which ends. Contents Toggle Main Menu 1 Sequences 2 The Summation Operator 3 Rules of the Summation Operator 3.1 Constant Rule 3.2 Constant Multiple Rule 3.3 The Sum of Sequences Rule 3.4 Worked Examples 4 Arithmetic sequence 4.1 Worked Examples 5 Geometric Sequence 6 A Special Case of the Geometric Progression 6.1 Worked Examples 7 Arithmetic or Geometric? 7.1 Arithmetic? 7.2 Geometric? 8 Simple and Compound Interest 8.1 Simple Interest 8.2 Compound Interest 8.3 Worked Examples 9 Video Examples 10 Test Yourself 11 External Resources SequencesĪ sequence is a list of numbers which are written in a particular order.


 0 kommentar(er)
0 kommentar(er)
